Model-based Machine Learning

Machine learning is the branch of artificial intelligence that deals with the problem of building automated systems that can learn from data with little human supervision. For this, most machine learning methods attempt to extract knowledge from the data by finding patterns that generalize. That is, patterns that are likely to occur in data instances that have not been observed. A successful machine learning system may use these patterns for making predictions about new data. An example of this is a system that is trained on email messages to learn to distinguish between spam and non-spam messages. In the learning process this system may identify which words are more likely to occur in spam messages. After learning, the system may use these words to classify new messages into spam and non-spam email folders.

In most machine learning systems the patters found in the data are summarized in terms of  a function that is used to discriminate between data instances. The precise form of this function is obtained during the learning phase. However, a key aspect of machine learning systems is this function representation. Typically, it is determined by the machine learning algorithm or model employed for learning. For example, if the model employed is a decision tree, the discriminative function will split the observed data at each node, starting at the root, until a leaf node  is reached. Similarly, a different model could specify that the discriminative function belongs to the family of second order polynomials.

Decades of research in machine learning have generated a multitude of different machine learning models that can be used for different learning tasks. To address a new learning problem, a practitioner often tries to map the problem to one of these methods. This may work well in certain situations. However,  in general, a tailored solution that is specifically formulated for each new application is expected to be better. The reason is that it may take advantage of specific details of the learning problem that more general methods may ignore. This is known as model-based machine learning and for its effective application it requires that the specific model is described in a machine-readable form.

The Bayesian Approach to Machine Learning

Discriminative functions are often determined in terms of a set of model parameters. In many traditional machine learning algorithms,  the learning process finds point values for these parameters by minimizing a cost function that is evaluated on the training data. This differs from the Bayesian approach in which the unknown parameters of the model are described using degrees of belief which are represented using probability distributions. These distributions or degrees of belief are then updated using Bayes’ theorem after the data has been observed.

The use of probabilities to represent and manipulate degrees of belief  in the Bayesian approach is supported by the Cox axioms. Specifically, it is possible to show that if some beliefs satisfy these simple consistency rules they can be mapped onto probabilities. Additionally, if our beliefs violate the rules of probability, the Dutch Book argument states that if we are willing to accept bets with odds based on the strength of our beliefs, there always exists a set of bets (called a “Dutch book”) which we will accept but which will make us lose money eventually.

The Bayesian approach fits nicely inside the framework described before. In order to describe the  model, one simply has to specify the prior beliefs about the different unknown parameters and the mechanism that is assumed to generate the observed data. Given this description and the data, Bayes’ rule is used to update our prior beliefs. A practical difficulty is however that Bayes’ rule becomes intractable in most real applications and one has to resort to approximate computations. These can be easily automated by using probabilistic programming languages that aim to unify general purpose programming with probabilistic modeling. Examples of these include Infer.NET and Church.

What is my research about?

During the last years my research has focused mostly on the Bayesian approach to machine learning. In this context, I have carried out several investigations in which the problem of feature selection and group feature selection has been considered. This includes learning problems where only a few of the observed attributes are actually relevant for prediction. Identifying a small sub-set of relevant attributes has broad applications, including the identification of bio-markers for early diagnosis or disease treatment. Besides this topic, I have also contributions in the field of ensemble learning, which deals with the problem of generating and blending many different classifiers to obtain improved prediction results. Non-parametric Bayesian models have also received my attention. In particular, I have worked with Gaussian processes, focusing on obtaining robust predictions in the presence of noise in the labels. Finally, I am also interested in the problem of causal inference, in which given two random variables, one has to determine if the first variable causes the second, or the second variable causes the first.

In my inverstigations I have mainly employed probabilistic models, relying on deterministic methods for approximate inference that scale well to large datasets and that are competitive with optimization methods.  The result of all this work has been published at top journals (e.g. Journal of Machine Learning Research and IEEE Transactions on Pattern Analysis and Machine Intelligence) and top conferences (e.g. NIPS or IJCAI).  Below there is a description of a selection of my research, classified in different topics, with links to the the most relevant publications considered by me.

Ensemble Pruning

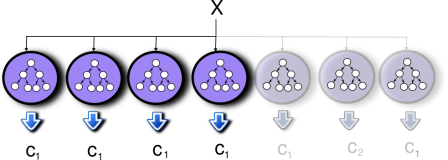Ensemble methods deal with the problem of generating and combining several classifiers with the aim of improving prediction performance. The effectiveness of these techniques is supported by different machine learning challenges, where they have obtained remarkable results. An example is the netflix prize challenge, where the winning solution blended several models for estimating movie ratings by users. Notwithstanding, besides this advantages in terms of prediction performance, ensemble methods also present some disadvantages in the form of increased storage space and longer prediction times than regular machine learning systems. I have investigated different ensemble pruning methods that attempt to reduce the size of the ensemble (and hence the storage space) by removing some of its elements. In contrast to what one should expect initially, removing these elements from the ensemble does not deteriorate the performance and, sometimes, it even leads to an improvement in the prediction accuracy. My research has also shown that it is not necessary to query all the classifiers in the ensemble to obtain a final decision. If the first classifiers in the ensemble already agree in their predictions, the final ensemble prediction is unlikely to be modified by the predictions of the remaining classifiers. This leads to a set of dynamic pruning methods which early stop the voting process of the ensemble saving prediction time.

• Martínez-Muñoz G., Hernández-Lobato D. and Suárez A. An Analysis of Ensemble Pruning Techniques Based on Ordered Aggregation IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 2, pp. 245-259, February, 2009. [pdf]

• Hernández-Lobato D., Martínez-Muñoz G. and Suárez A. Statistical Instance-Based Pruning in Ensembles of Independent Classifiers IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 2, pp. 364-369, February, 2009. [pdf]

Bayesian Infernece in Sparse Linear Models

Many learning problems are characterized by a large number of explaining attributes or features and by a small number of observed data instances. Under these circumstances, even a linear model is too complex and may over-fit the training data. A natural approach to alleviate this problem is to assume that only a few of the attributes are relevant for prediction. This is equivalent to the assumption of many zeros in the coefficients of a linear model, i.e., the coefficients are sparse. This prior knowledge can be introduced by setting for the model coefficients a sparse enforcing prior distribution. Examples of these distributions include the Laplace, the horseshoe and the spike-and-slab. These distributions have a high probability mass at or near zero to favor sparse solutions, but also allow for values that are significantly different from zero to account for relevant attributes for prediction. My research has analyzed the suitability of these priors combined with a Bayesian approach for sparse inference in linear regression models. The results obtained indicate that deterministic methods for approximate inference can be employed in these models, and that they are competitive with other mahcine learning methods based on optimization. Furthermore, the incorporation of some structure information in the sparsity patterns of the solutions has also been investigated, showing that it can lead to a significantly improvement in the prediction performance and in the reconstruction of the model coefficients. Further research work shows that these strucutres can be represented by dependencies in the feature selection process and that these dependencies can be inferred from the training data alone. This is a very important result because most methods assume that the information structure about the possible sparsity patterns of the model coefficients is given by some expert beforehand.

• Hernández-Lobato D., Hernández-Lobato J. M. and Dupont P. Generalized Spike-and-Slab Priors for Bayesian Group Feature Selection Using Expectation Propagation Journal of Machine Learning Research. 14(Jul):1891−1945, 2013 [pdf] [R-Code]

• Hernández-Lobato D., Hernández-Lobato J. M. Learning Feature Selection Dependencies in Multi-task Learning Advances in Neural Information Processing Systems (NIPS), Tahoe, USA, 2013, Pages 746-754[pdf][R-Code & Sup. Material]

Robust Guassian Process Classification

Gaussian process classifiers are non-parametric machine learning methods. This means that given enough data, they can be use to accurately describe any classification problem. Furthermore, Gaussian processes can be understood as probability distributions over functions. In this case, the function that is used to discriminate among different class labels. Such distributions over functions have the property that, given any finite-dimensional set of points onto which the discriminative function should be evaluated, the function values follow a multi-variate Gaussian distribution. Extensive research with these models has shown that they perform very well in diverse learning tasks. However, a drawback of Gaussian processes for classification is that they are strongly influenced by outliers, i.e., noisy data instances that do not share the same patterns as the majority of the data instances observed.  As a matter of fact, these instances can affect the learning process and lead to severe over-fitting, and hence, to a reduced prediction accuracy of the resulting classifier. In this context, my research has investigated different methods that can be used for Gaussian processes classification to alleviate the influence of this instances during learning. In particular, a robust version of a Gaussian process classifier has been described and analyzed both for binary and multi-class problems. The results obtained indicate that such a model performs significantly better in the presence of labeling noise. Additional investigations show that privileged data, i.e., data that is only available at training time, can also be used to provide better generalization results in this type of classifiers.

• Hernández-Lobato D. and Hernández-Lobato J. M. Bayes Machines for Binary Classification Pattern Recognition Letters, Volume 29, Issue 10, 15 July 2008, Pages 1466-1473, ISSN 0167-8655.[pdf]

• Hernández-Lobato D., Hernández-Lobato J. M.,  and Dupont P. Robust Multi-Class Gaussian Process Classification Advances in Neural Information Processing Systems (NIPS), Granada, Spain, 2011, Pages 280-288 [pdf] [R-Code & Sup. Material]

• Hernández-Lobato D., Hernández-Lobato J.M., Quadrianto N. Robust Gaussian Process Classification using Privileged Information Submitted to Neural Information Processing Systems (NIPS), 2014.

Causal Inference

The problem of causal inference assumes that there are some samples of two random variables that are observed and it consists in determining whether it is the first variable that causes the second (i.e., X→Y) or it is the second variable that causes the first (i.e. Y→X). In general this problem has no solution. However, in certain situations, and under certain assumptions, it is possible to derive some asymmetries between the model in one direction and the model in the opposite direction that can be exploited to determine the causal direction. This problem has been analyzed in the context of vector auto-regressive models finding empirical evidence that suggest that the residuals (i.e., by how much the predictions of the model are incorrect) in the wrong direction are more Gaussian than in the right causal direction. This means that statistical tests based on the levels of Gaussianity can be used for causal inference in this type of models. Several experiments show that these tests lead to improved prediction results when compared to statistical tests based on the independence of the residuals with respect to the observations.

• Morales-Mombiela P., Hernández-Lobato D., and Suárez A. Statistical Tests for the Detection of the Arrow of Time in Vector Autoregressive Models Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing 2013, pages 1544-1550 [pdf]

Research Profiles

Below you can find automatically generated summaries of my research work. Take a look at them! The profile generated by google scholar has free access, but in order to access the others you may require a suscription.